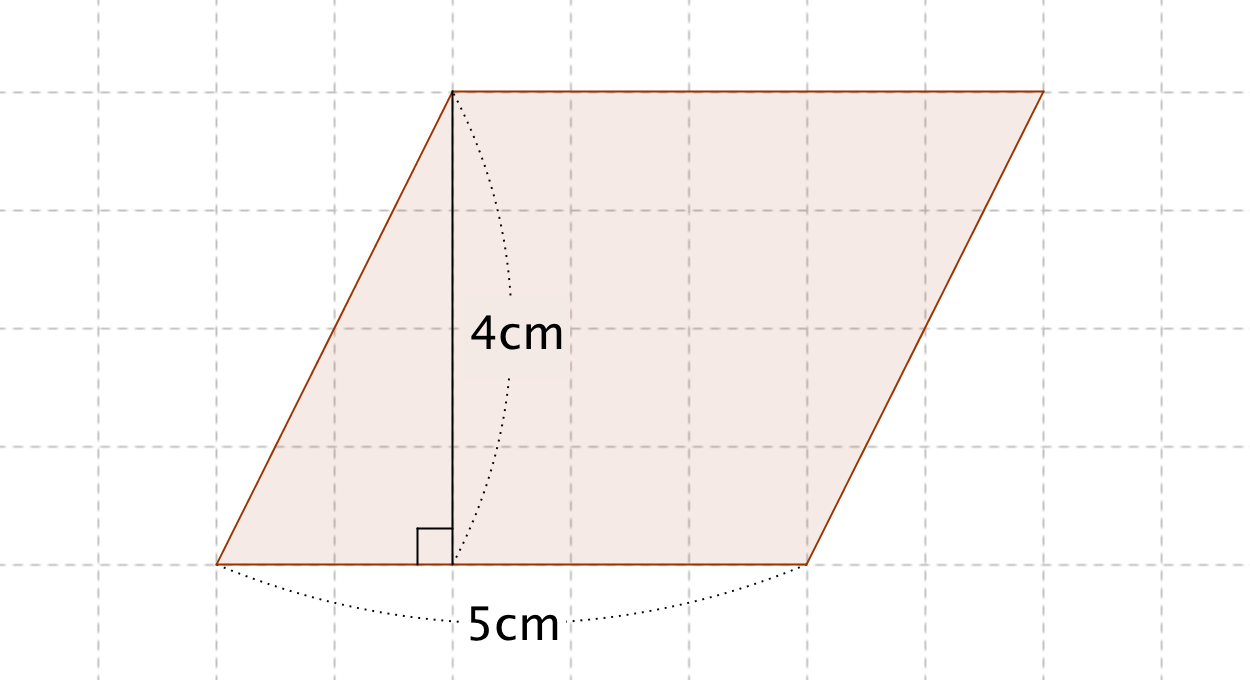
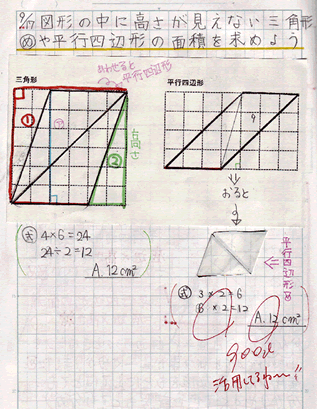
17/2/21 平行四辺形 高さ 求め方 中学つまり、この平行四辺形では、高さは底辺に垂直な\ (5cm\)のところとなります。 平行四辺形の面積は、\ (8\times 5=40\)となります。23/7/19 例1)2つの三角形に分けて求めます。 *高さがどこになるか注意しましょう。 例2)下のような土地に道が通っているとき、色のついた部分の面積を求めます。 はしに寄せて考えます。 平行四辺形と長方形の面積は同じになるので、平行四辺形の道の面積も右端に寄せてしまいます。この場合,回転体は半径2cm,高さ4cmの円柱になるので,その体積Vは V=底面積×高さ=2×2×π×4= 16π cm 3 となります. これをパップス・ギュルダンの定理を使って解いてみます. 「 断面積 」は縦4cm,横2cmの長方形なので 2×4=8 cm 2 です. 「 断面の
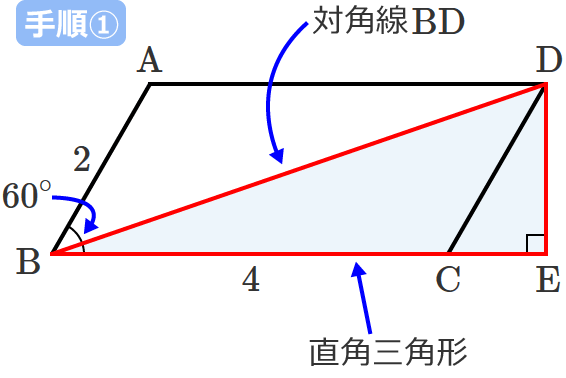
平行四辺形の対角線の長さの求め方
平行四辺形 高さ 求め方 中学
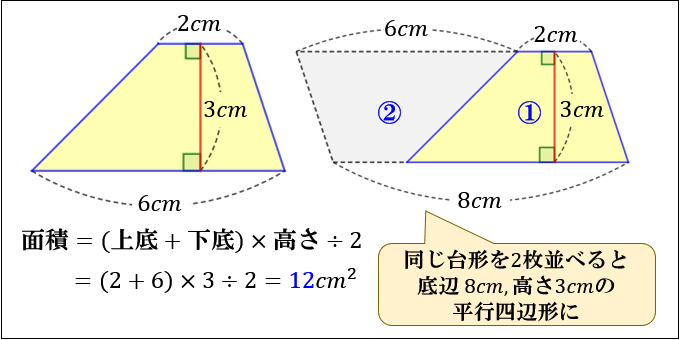
平行四辺形 高さ 求め方 中学- また、問題の解き方も簡単に解説していくので、ぜひこの記事を通してマスターしてくださいね! 目次 非表示 中点連結定理とは? 中点連結定理の使い方例題 中点連結定理の証明 証明①三角形の相似を利用 証明②平行四辺形の性質を24/6/ 台形の面積は「平行四辺形の面積」を利用すれば求められます。 ある台形と同じ形の台形をくっつけると、大きな平行四辺形になります。 ((図)) 平行四辺形の面積は「底辺×高さ」でしたが、この平行四辺形の面積はどうなるか考えると



教育ソフト開発研究所 5年5巻
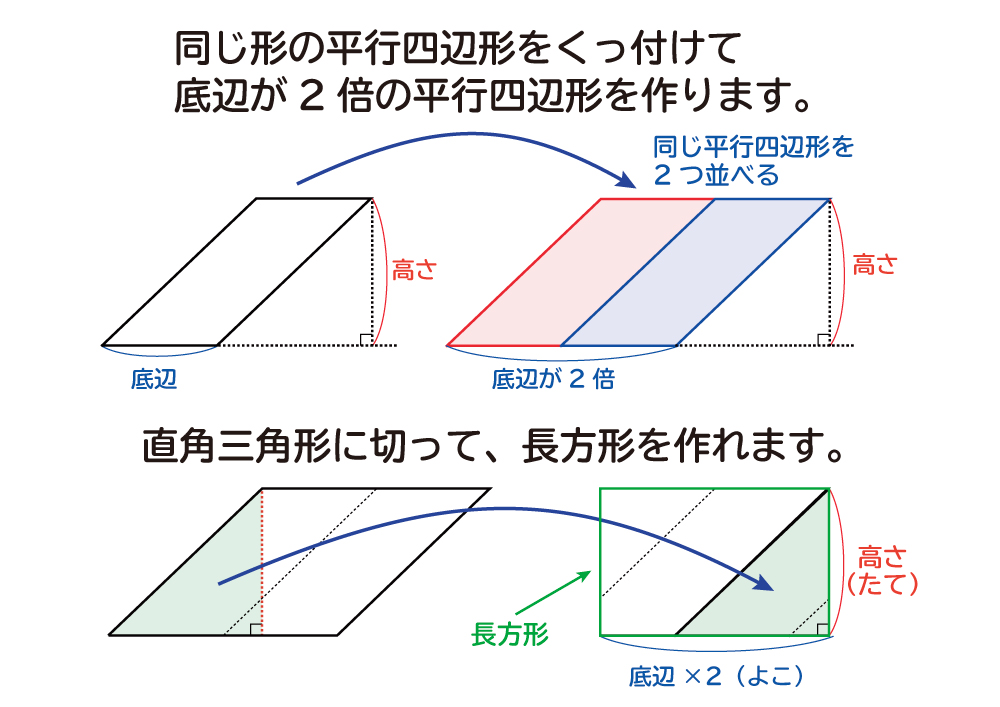
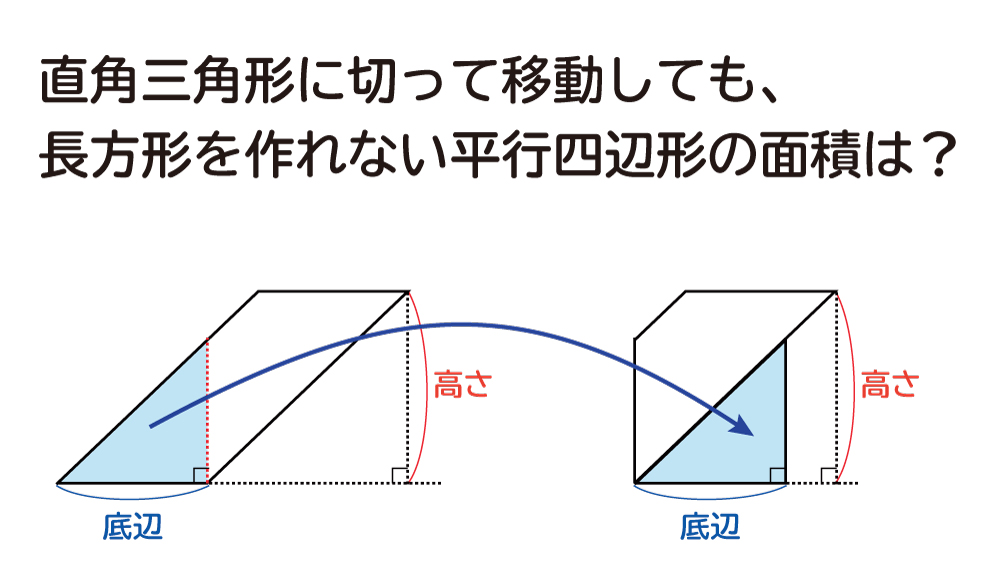
1/3/18 今回は、平行四辺形の面積の求め方について書いていきたいと思います。 平行四辺形の面積を求める公式 平行四辺形の面積を求める問題 問題① 《平行四辺形の面積の求め方》 問題② 《平行四辺形の面積の求め方》 問題③ 《平行四辺形の高さの求め方》 問題④ 《平行四辺形の底辺の求め方3/8/ となり、前に示した(上底下底)×(高さ)×\(\frac{ 1 }{ 2 }\)になってることが確認できますね。 台形の面積の公式の証明② 2つめの証明は 元の台形に合同な台形を逆さにしてくっつけ、平行四辺形を作るやり方 です。 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m
000 / 1 • Live • 三角形と四角形の面積の求め方を覚えましょう。 三角形の面積=底辺×高さ÷2 ※ 「高さ」がどの部分の長さなのかをていねいに考えて下さい。 長方形の面積=たて×よこ 正方形の面積=1辺×1辺 平行四辺形の面積=底辺×高さ新しい 平行四辺形 三角形 面積 高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry 平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 平行四辺形の中の三角形の面積 算数に関する質問 勉強質問サイト 平行四辺形と三角形の面積 立方体の中にある三角すい たくさんの中学で出題されている問題です。 高さが2cmの二等辺三角形4つを切り取ってできたものです。 これを組み立ててできる四角すいの体積を求めなさい。 ただし、角すいの体積は、 (底面積)× (高さ)÷3で求められます
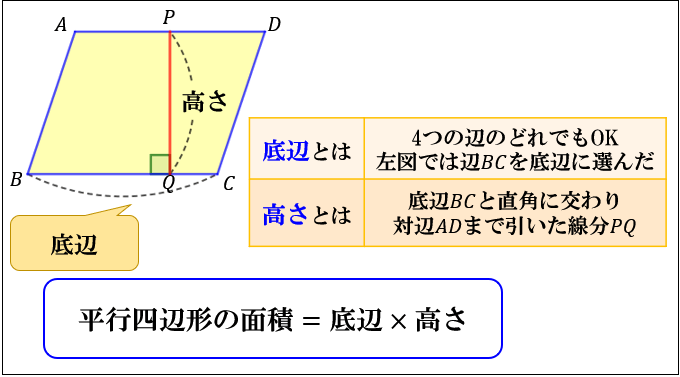
今回は平行四辺形の高さが外にある場合の指導です。 まず、高さを予想して、それが正しいか証明するといった流れで実践しました。 では、指導実践です。 まずは、平方四辺形の面積の求め方を確認しました。三角形の面積高さ固定 解説 三角形の面積高さ固定(音つき) 解説 平行四辺形の面積 解説 平行四辺形の面積2 解説 三角形と平行四辺形と台形 三角形の面積 平行四辺形の面積 台形の面積 解説 三角形の面積 解説 面積の公式(小数点の掛け算を使って19/6/17 2つを使う平行四辺形の問題 その両方の面積比の法則を使う代表的な問題が、この平行四辺形の各面積比の問題です。 平行四辺形abcdがある。相似な図形を探す。 この平行四辺形をつくっている三角形3つと四角形1つの面積比を求めてみます。




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
こちらの記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。 正方形であれば、一辺の長さが2倍になると面積が4倍になります。上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積 平行四辺形の面積は、 底辺×高さ で計算します。下図のように、平行四辺形に垂直線を引きます。できた三角形を右側にスライドさせるとピッタリはまります。12/5/21 周りの長さ を聞かれることもよくあるので、図形を思い浮かべてみよう! 平行四辺形の面積=底辺×高さ 平行四辺形の周りの長さ=(縦+横)×2 台形の面積=(上底+下底)×高さ÷2 ひし形の面積=対角線×もう一方の対角線÷2 ひし形の周りの長さ




平行四辺形の面積 簡単に計算できる電卓サイト
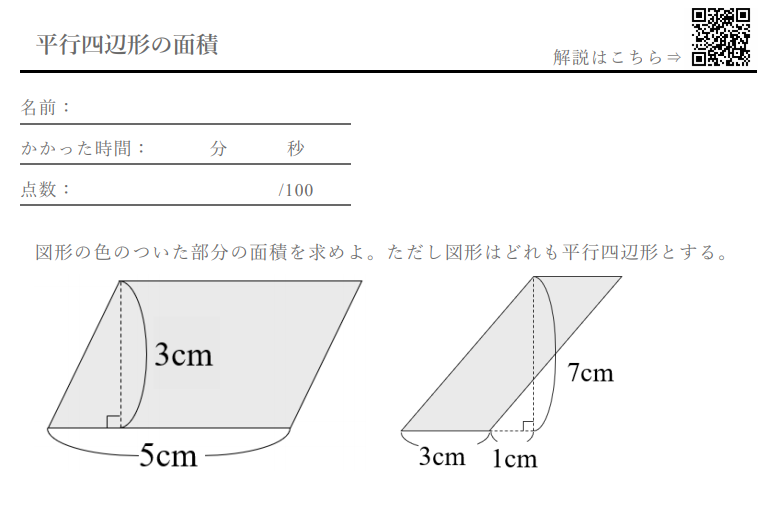



平行四辺形 の面積 計算ドリル 問題集 数学fun
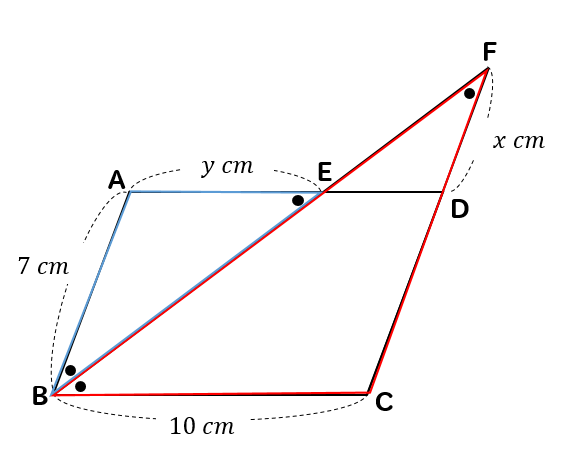
三角形の面積 = \(\large{\frac{1}{2}}\)×底辺×高さ ですね 形は変われど、「\(\large{\frac{1}{2}}\) 」も「底辺」も「高さ」も変わっていませんものね!17/8/ 平行四辺形の面積の求め方についてです。 平行四辺形の面積は、 「底辺×高さ」 で求めることができます。 証明はとても簡単です。平行四辺形を面積を変えずに長方形の形にするという方法です。 長方形の面積の求め方は「たて×横」でしたね。6/2/14 ③eの座標は求めなくてもできるので割愛。一応 e(5/2,3)ですが。 ④ aedの面積を求める, 底辺ed=5/2 高さはaからbdに垂線をおろして 3 よって, aed=(1/2)×(5/2)×3=15/4 ⑤平行四辺形abcdは, aedの4倍 だから, (15/4)×4=15(答) です。




面積 平行四辺形の面積 01 高さが外にあるときの面積の求め方 Youtube



1
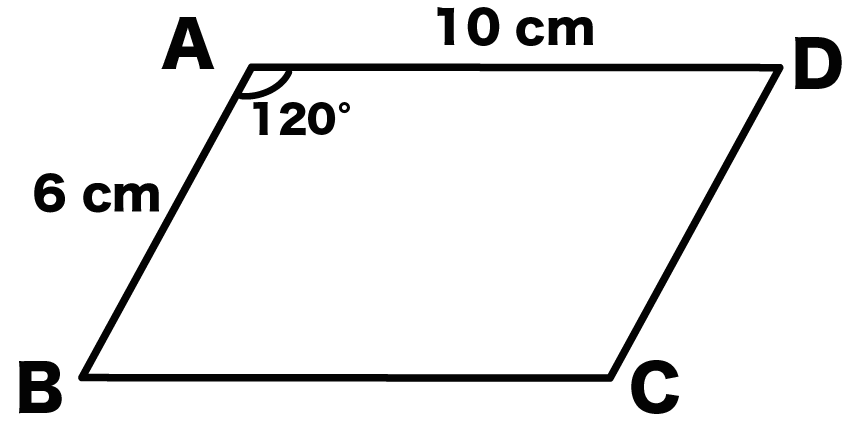
底辺×高さ っていう公式がつかえるんだろう?? じつはこれは、 ひし形が平行四辺形であるから なんだ。 ※詳しくはひし形の定義をみてね^^ 平行四辺形の面積は「底辺×高さ」で求められたよね?? 菱形は平行四辺形ともいえるから、2/4/19 平方四辺形を対角線で分けた $4$ つの三角形の面積は等しいから、平行四辺形の面積は、 $4\times \dfrac{3\sqrt{3}}{2} = 6\sqrt{3}$ だね! まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、 に質問があり、その日に回答、ベストアンサーを貰ってしまったのですが、僕にもわからず悩んでいた所があり、再質問します問題文: 図のように、平行四辺形の各辺の3等分点の一つと頂点を結んだ線を 引きます。網目部分の面
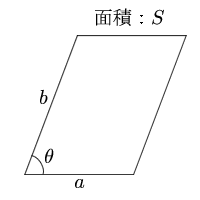



平行四辺形 2辺と間の角度 面積の計算 計算サイト




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
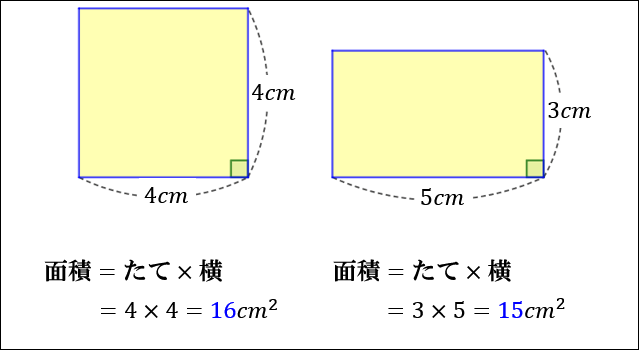
10/7/ 平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理:1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる※平行とは 1辺の異なる2つの場所から、もう1辺に線を垂直に下して、2つの垂直線が同じ長さであること <四角形の面積の求め方> 正方形・長方形・平行四辺形 底辺×高さ問題(7)解説! の値を求めなさい。 これは少し複雑ですね。 いくつかの相似な図形を辿りながら を求めていきます。 まずは、長さが与えられているAB、CDを含む ABEと DCEに注目します。 2つの図形は相似になっており AB:CD=6:9=2:3より 相似比は2:3だと分かります。 つまり、他の辺の比も2:3になるので




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
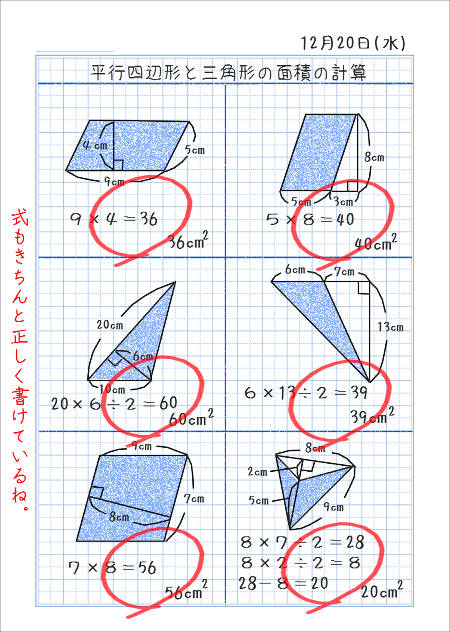



平行四辺形と三角形の面積 家庭学習レシピ
19/2/21 求めたい台形の高さは \(\mathrm{OE} \mathrm{OF}\) である。 三角形の面積を利用して、 \(\displaystyle \triangle \mathrm{AOD} = \frac{1}{2} \cdot 3 \cdot \mathrm{OE}\)ポイントに従って、平行四辺形の面積公式を使ってみよう。 中学校までは、(底辺)×(高さ)で求めたね。 数学Ⅰでは、(高さ)を 「(斜めの辺)×sin」 で表すよ。 四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
(平行四辺形の高さ)=(面積)÷(1辺の長さ) ってことだね。 たとえば、面積が36 cm^2、BCの長さが9 cmの平行四辺形があったとする。 このとき、平行四辺形の高さは、 (高さ)=(面積)÷(1辺の長さ) = 4 cm になるんだ。 このタイプの問題は公式をつかっていこう! 求底辺の長さ $a$、高さ $h$ の平行四辺形の面積 $S$ は、次の公式で求められます。 平行四辺形 (へいこうしへんけい) の面積 \begin{align*} S = ah \end{align*} 面積 = 底辺 × 高さ 公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「平行四辺形の面積の求め方」をご覧ください。8/8/19 こんにちは、ウチダです。 今日は、小学生から高校生まで通して学ぶ 「三角形の面積の求め方」 について、まずは基本から入り、徐々に高校数学の内容に進化させていきます。 具体的には、数学Ⅰで習う "sin" を用いる公式や、数学Bで習う "ベク



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




相似 平行四辺形と面積比の問題を徹底解説 数スタ
平行四辺形の面積を求めるときは、 (底辺) × (高さ) の公式から導く のではなく、 上記のような三角形を移動する考え方を頭の中でするけど、解答用紙に全部書くのめんどくさいから、 結論の (底辺) × (高さ) だけ をを書くっていう、思考回路です。 まとめ平行線と面積 等積変形 三角形の面積=底辺×高さ× 1 2 底辺の長さと高さがそれぞれ等しければ面積は等しくなる。 a b c p abcと底辺bcが共通の pbcがある。 abcと pbcの面積が等しい場合、両方の三角形の高さが等しいので >>高さ 直線apと直線bcは平行 になる




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の辺や角を求める Youtube




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




平行四辺形の面積の求め方 公式と計算例



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



教育ソフト開発研究所 5年5巻



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



算数道場 4 面積と体積 1 面積の意味と単位 その7 平行四辺形の面積



平行四辺形の面積の公式 算数の公式
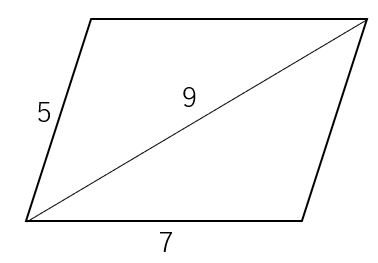



面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
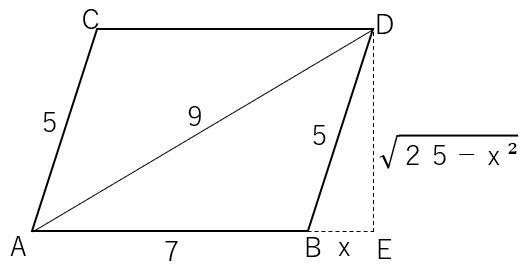



面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧
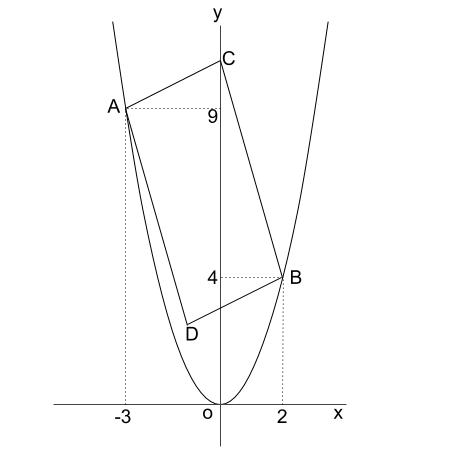



2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su
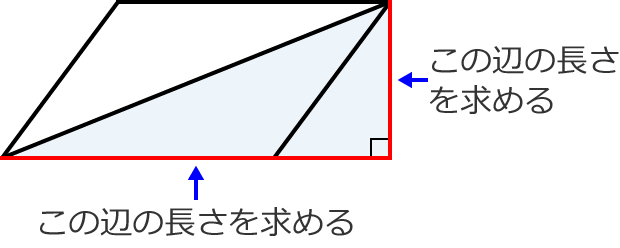



平行四辺形の対角線の長さの求め方



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
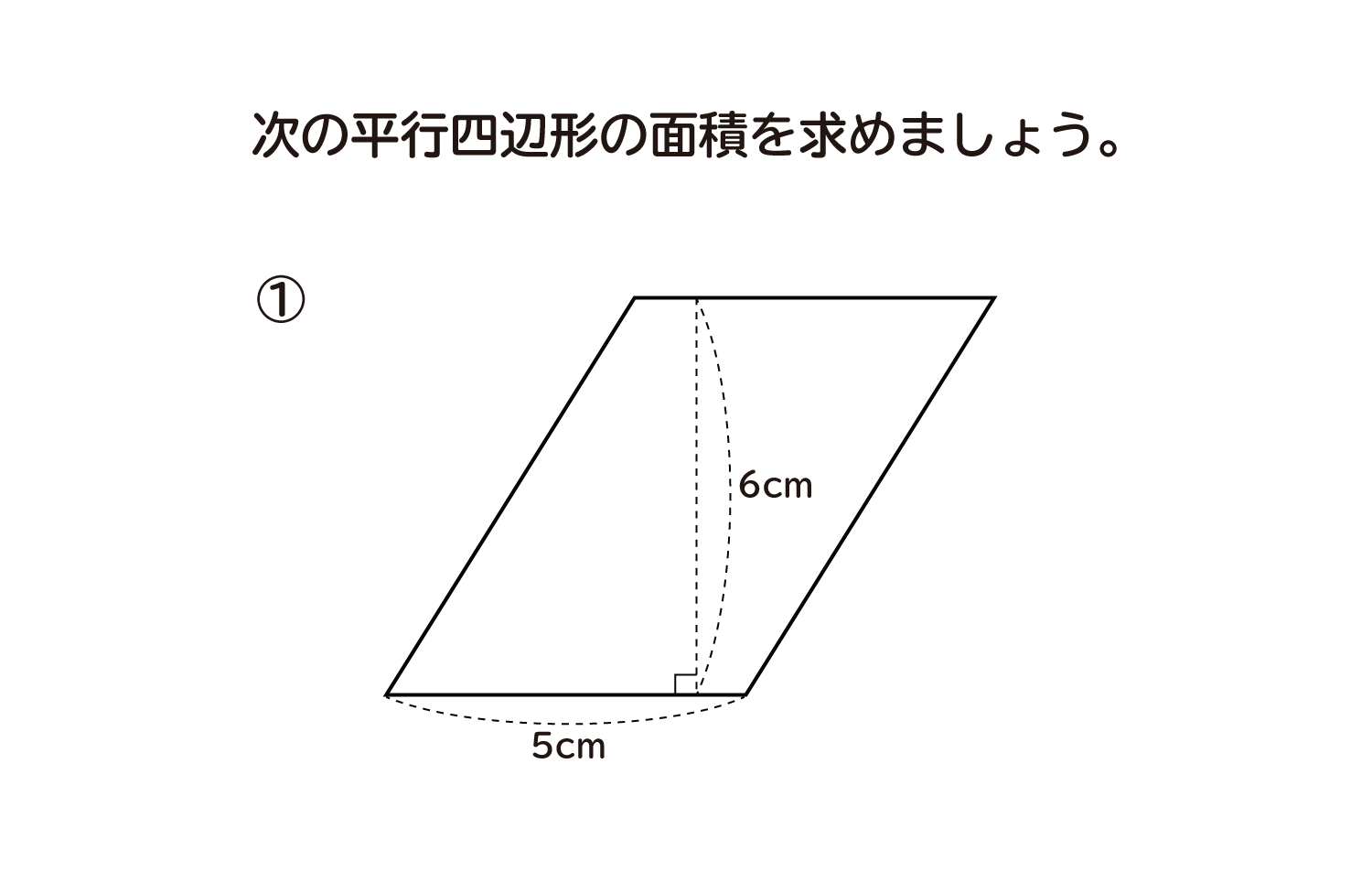



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル
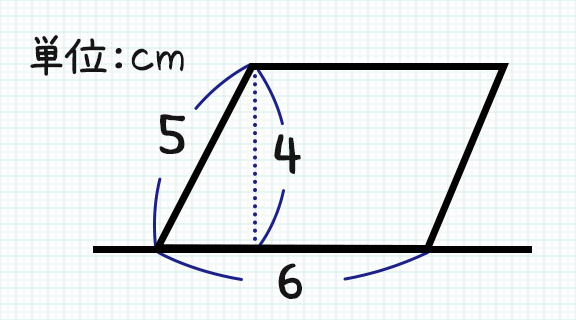



毎日脳トレ この平行四辺形の面積わかる Dアプリ レビュー
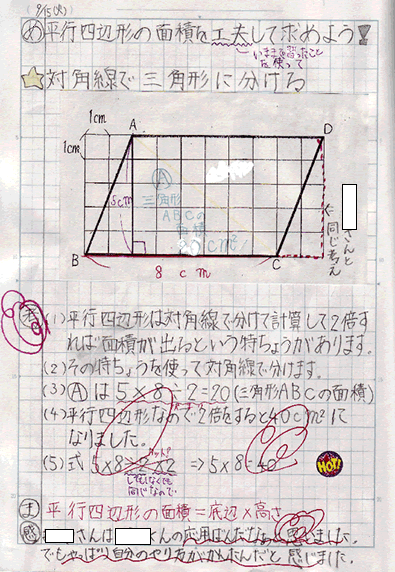



面積5 12の流れ




平行四辺形の対角線の長さの求め方




小5 算数 小5 41 平行四辺形の面積 Youtube




平行四辺形の面積の求め方 公式と計算例




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




平行四辺形の対角線の長さの求め方




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
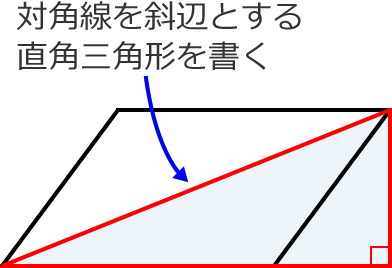



平行四辺形の対角線の長さの求め方




中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方



5年算数三角形と四角形の面積2 教え方 台形 ひし形




平行四辺形で知っておくべきこと 苦手な数学を簡単に




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



面積6 12の流れ
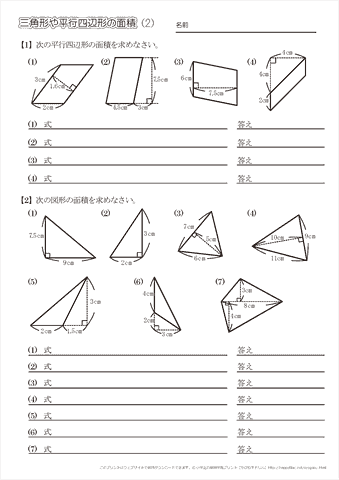



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




平行四辺形の面積の求め方 公式と計算例




平行四辺形の対角線の長さの求め方




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
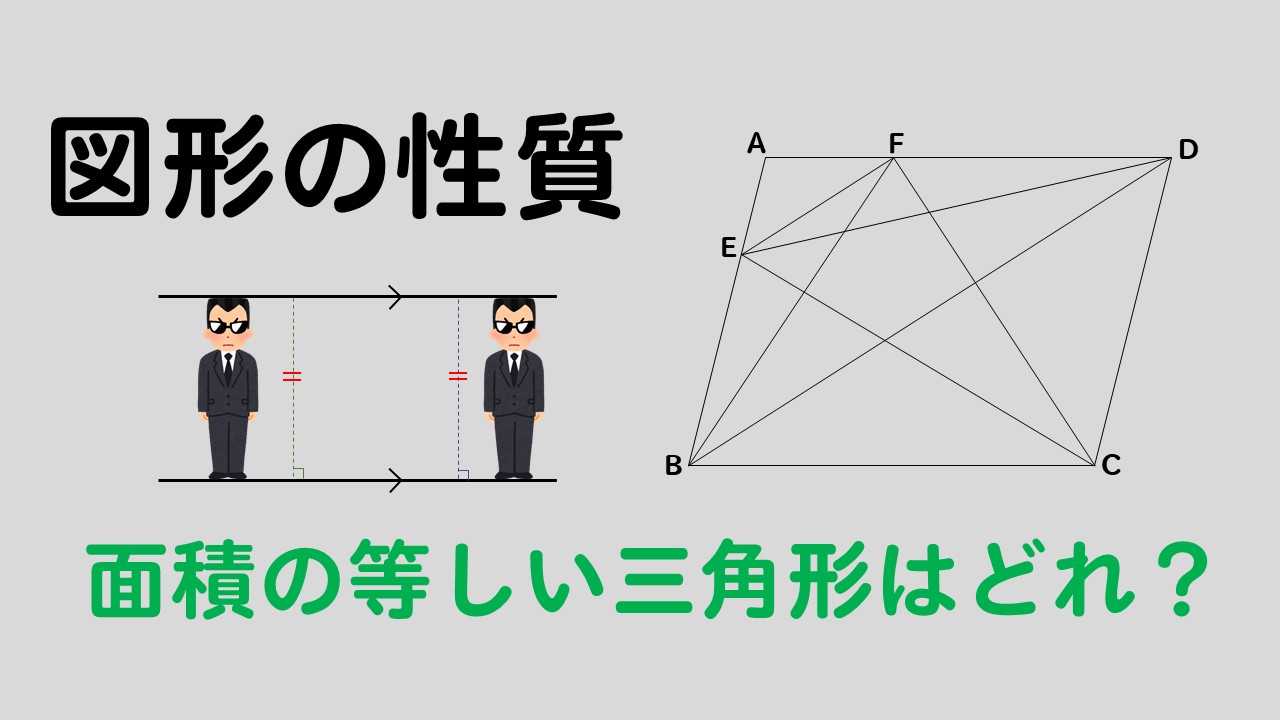



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ




中学受験算数 平行四辺形の面積を求める問題 Okwave




四角形と三角形の面積



1




5年 四角形と三角形の面積 ゲンタの授業ポートフォリオ
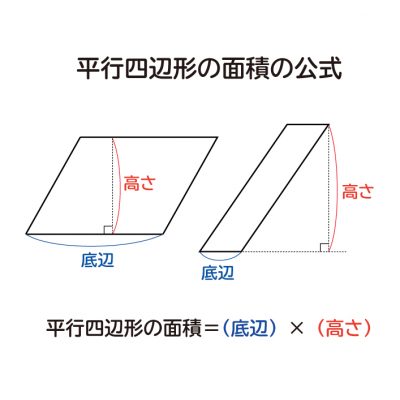



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
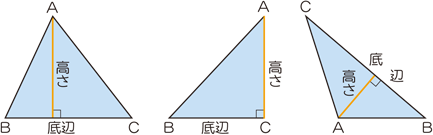



底辺と高さ 算数用語集



平行四辺形の高さの求め方を教えてください 底辺が6 面積が24 です 宜 Yahoo 知恵袋



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット
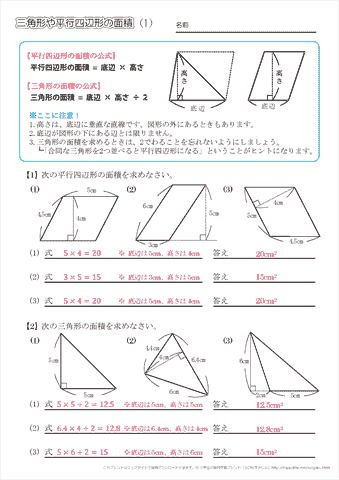



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




平行四辺形の面積の求め方 公式と計算例
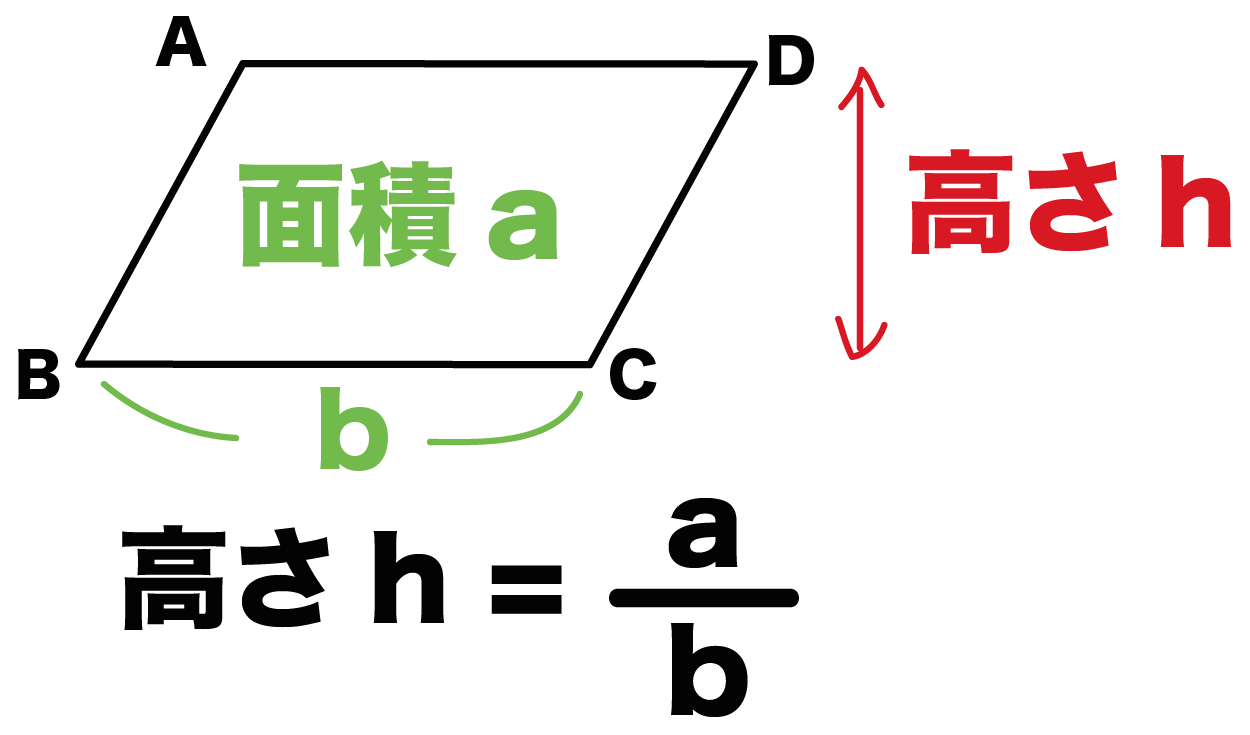



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく



1
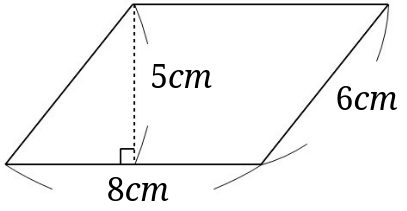



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校




平行四辺形の面積の求め方 公式と計算例




高さがわからない平行四辺形の面積の求め方 Youtube
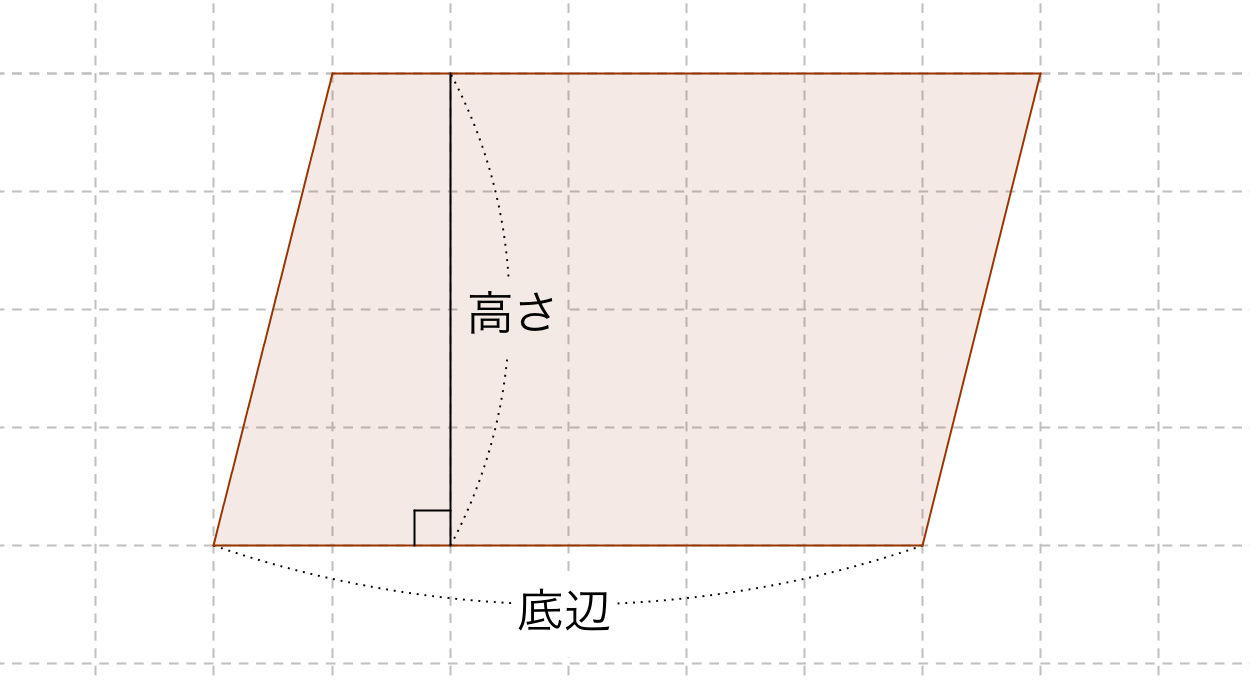



平行四辺形の面積の公式 算数の公式



四角形abcdは台形でabedは平行四辺形です 台形abcdの面積の Yahoo 知恵袋
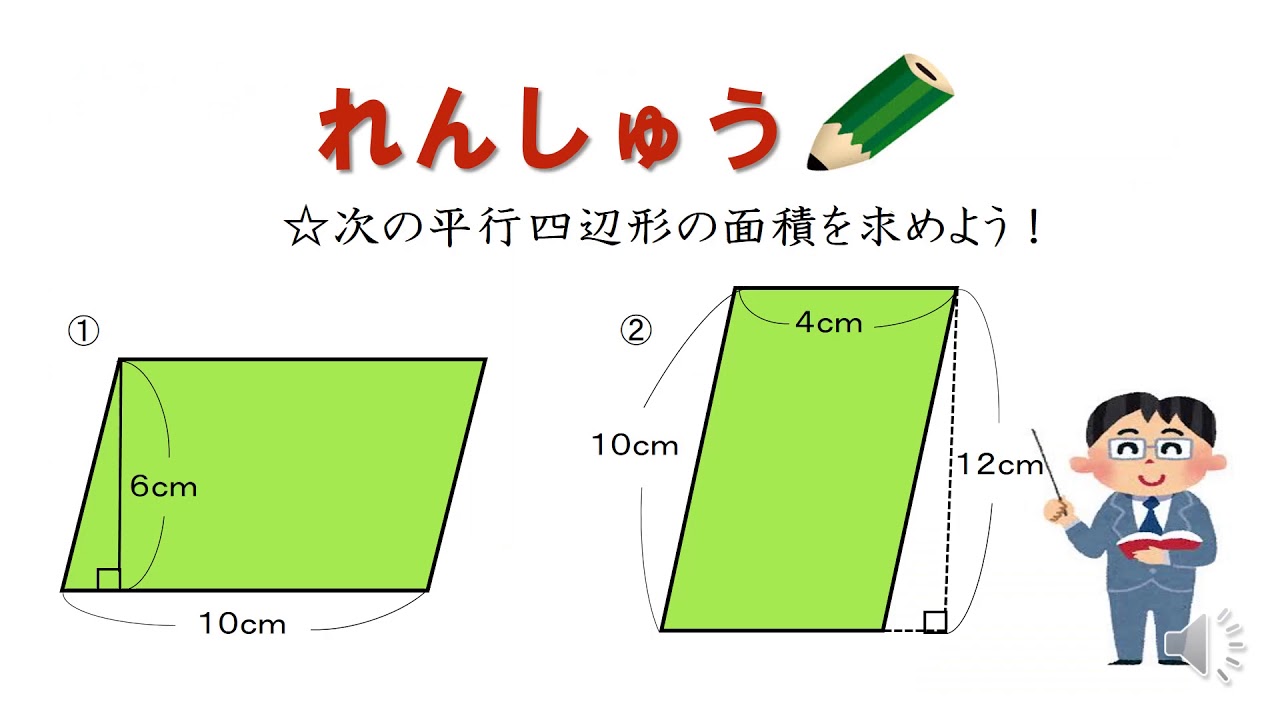



小5 面積の求め方を考えよう 平行四辺形 日本語版 Youtube



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校
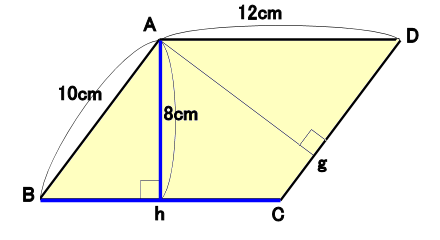



平行四辺形と高さ




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三角形の高さの求め方 底辺の位置によって 高さは変わる 中学や高校の数学の計算問題




小5 算数 小5 41 平行四辺形の面積 Youtube
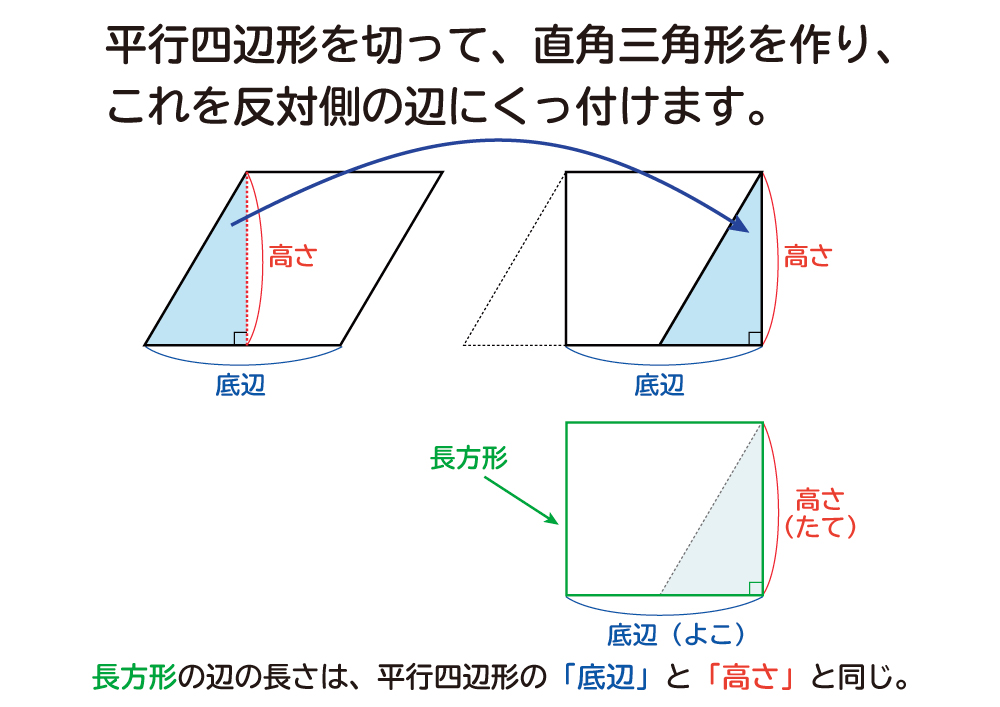



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル
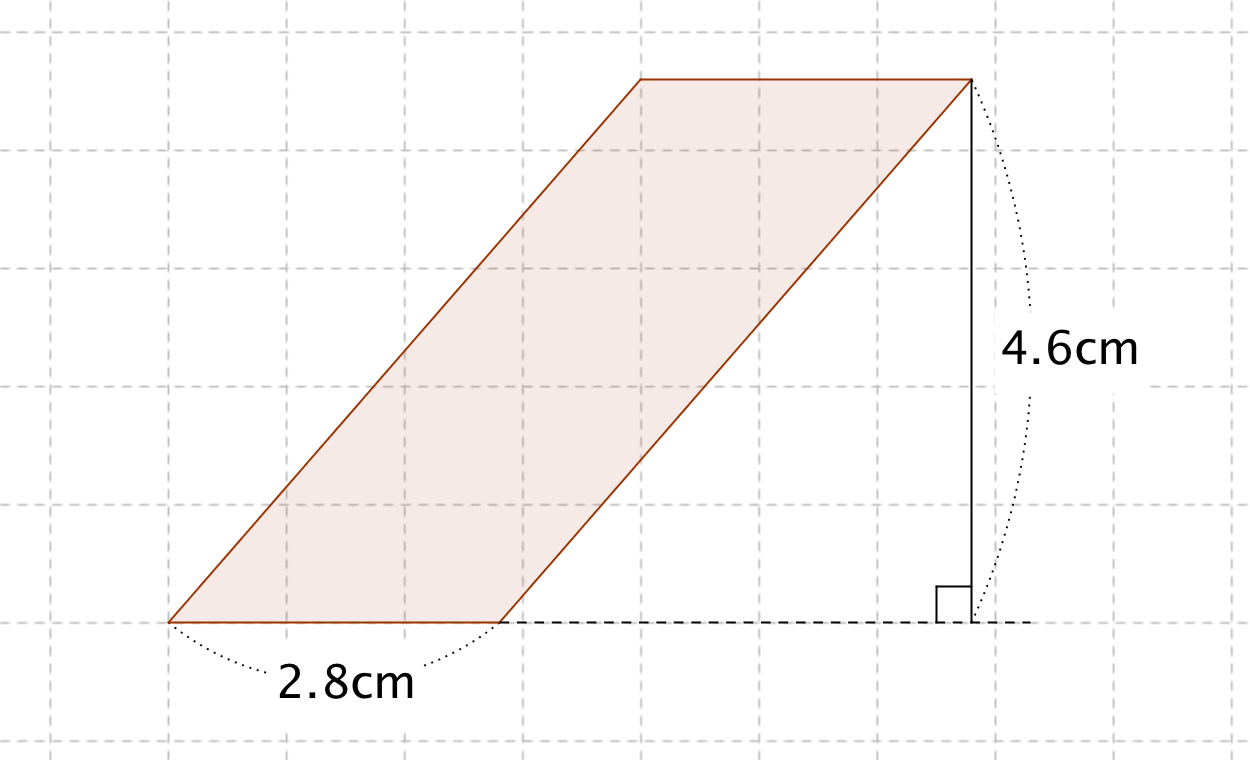



平行四辺形の面積の公式 算数の公式




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



平行四辺形対角線の求め方と面積について 対角線acの長さの Yahoo 知恵袋
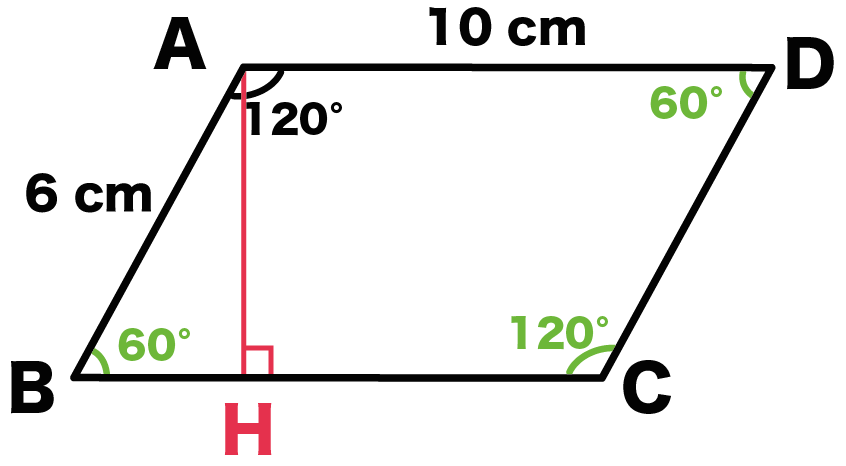



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく



数学 中2 73 平行四辺形の性質 Youtube




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori




相似 平行四辺形と面積比の問題を徹底解説 数スタ



高さの分からない平方四辺形の面積求め方教えて下さい 写真横ですみませ Yahoo 知恵袋



1




台形の面積の求め方 公式と計算例
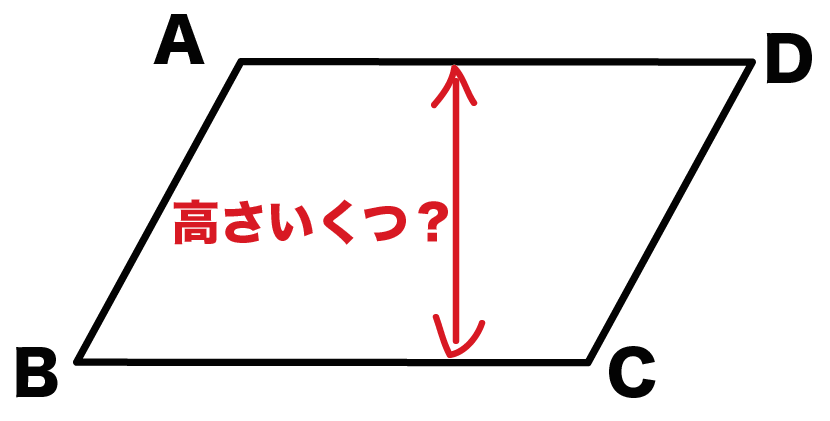



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿